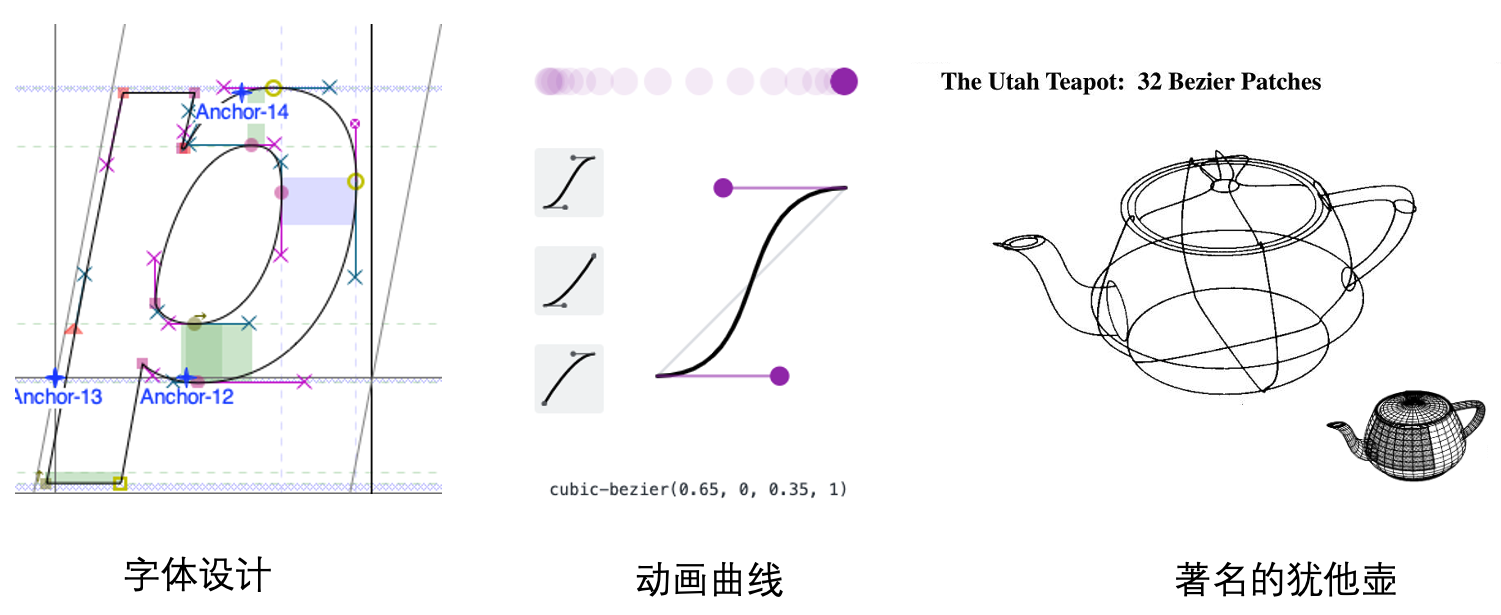
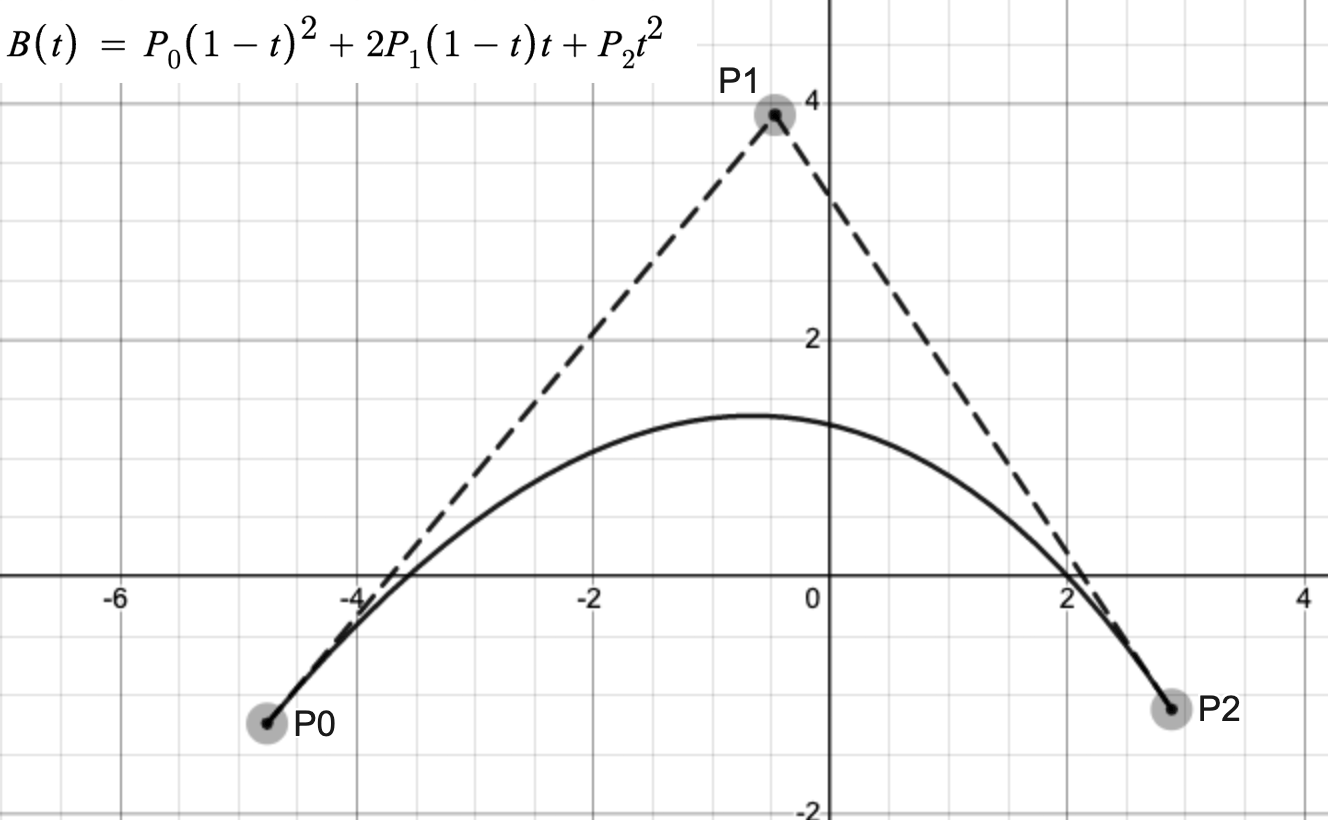
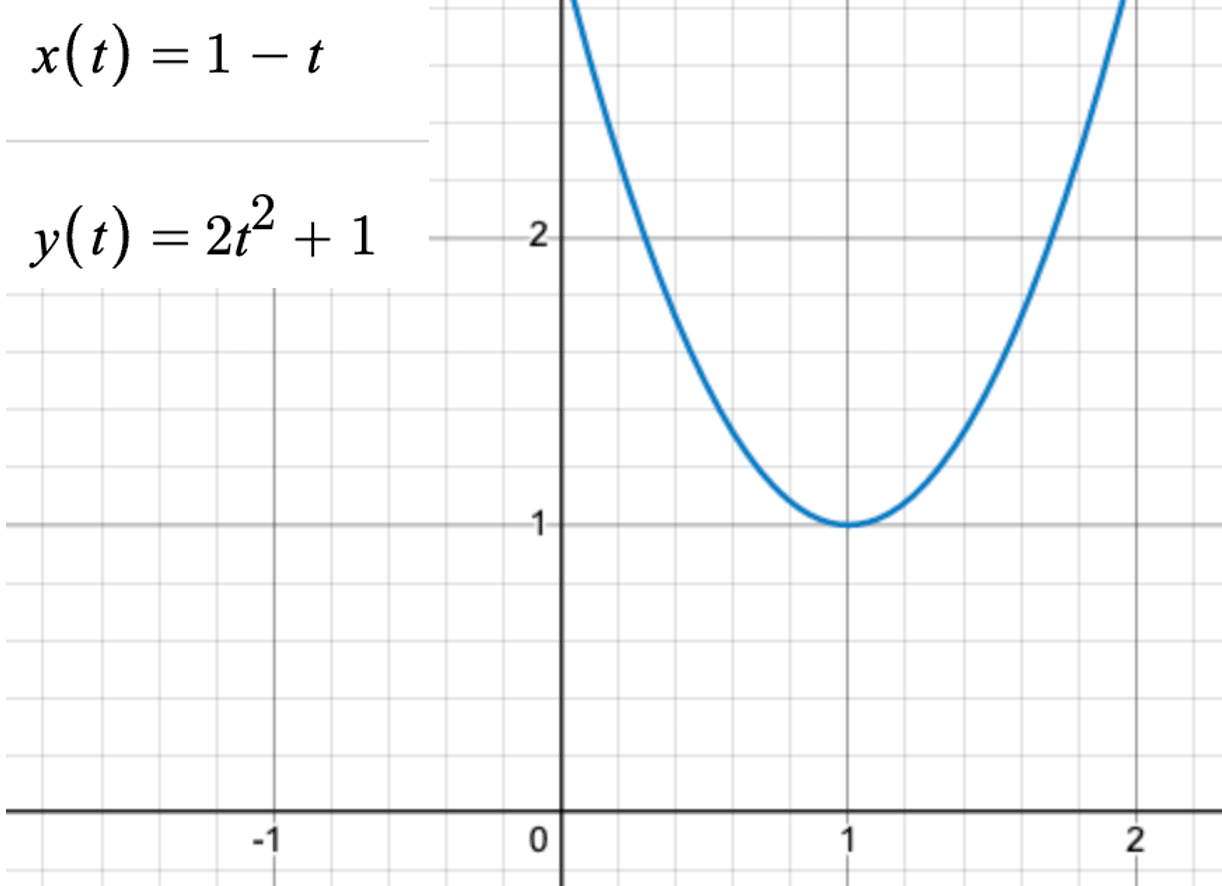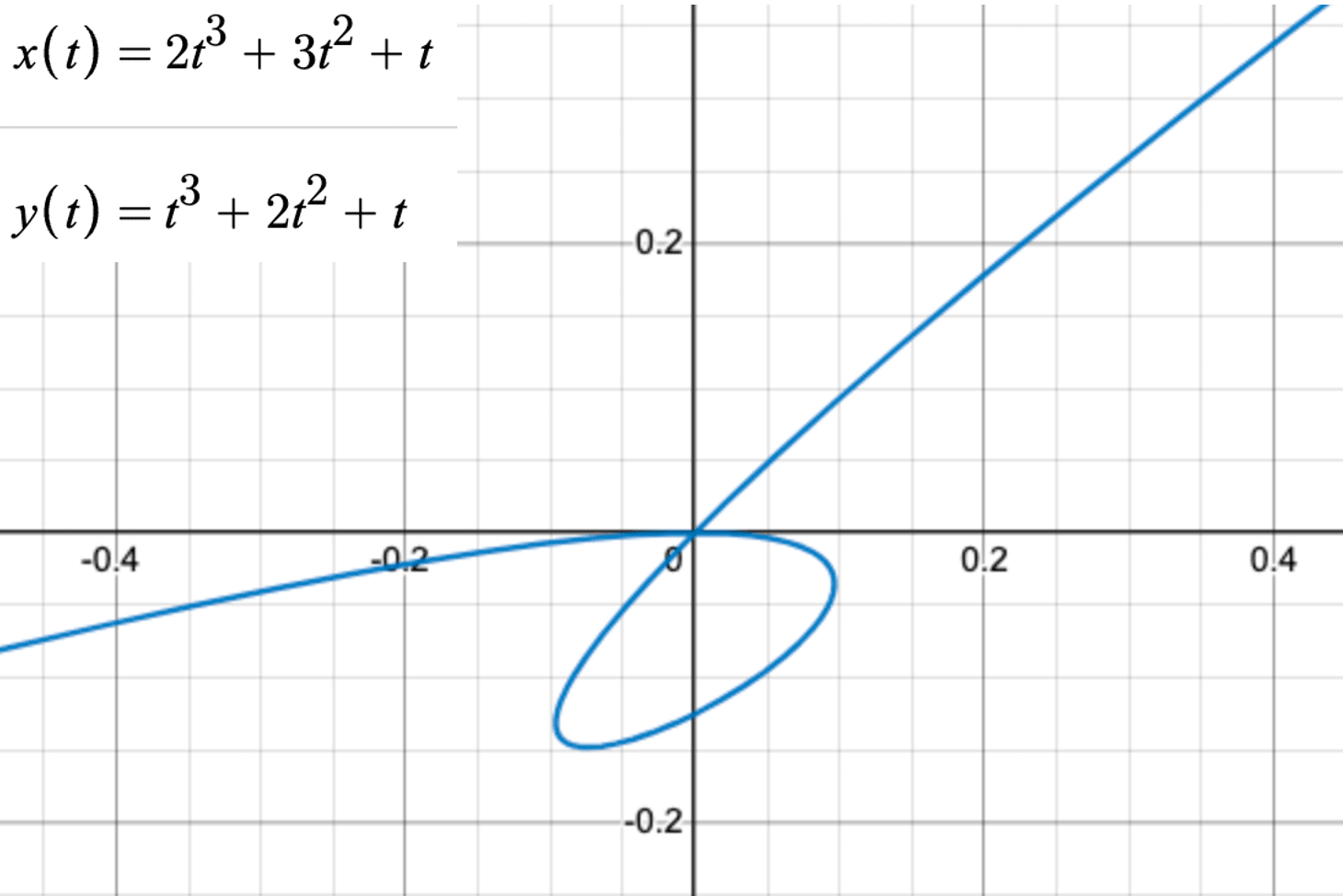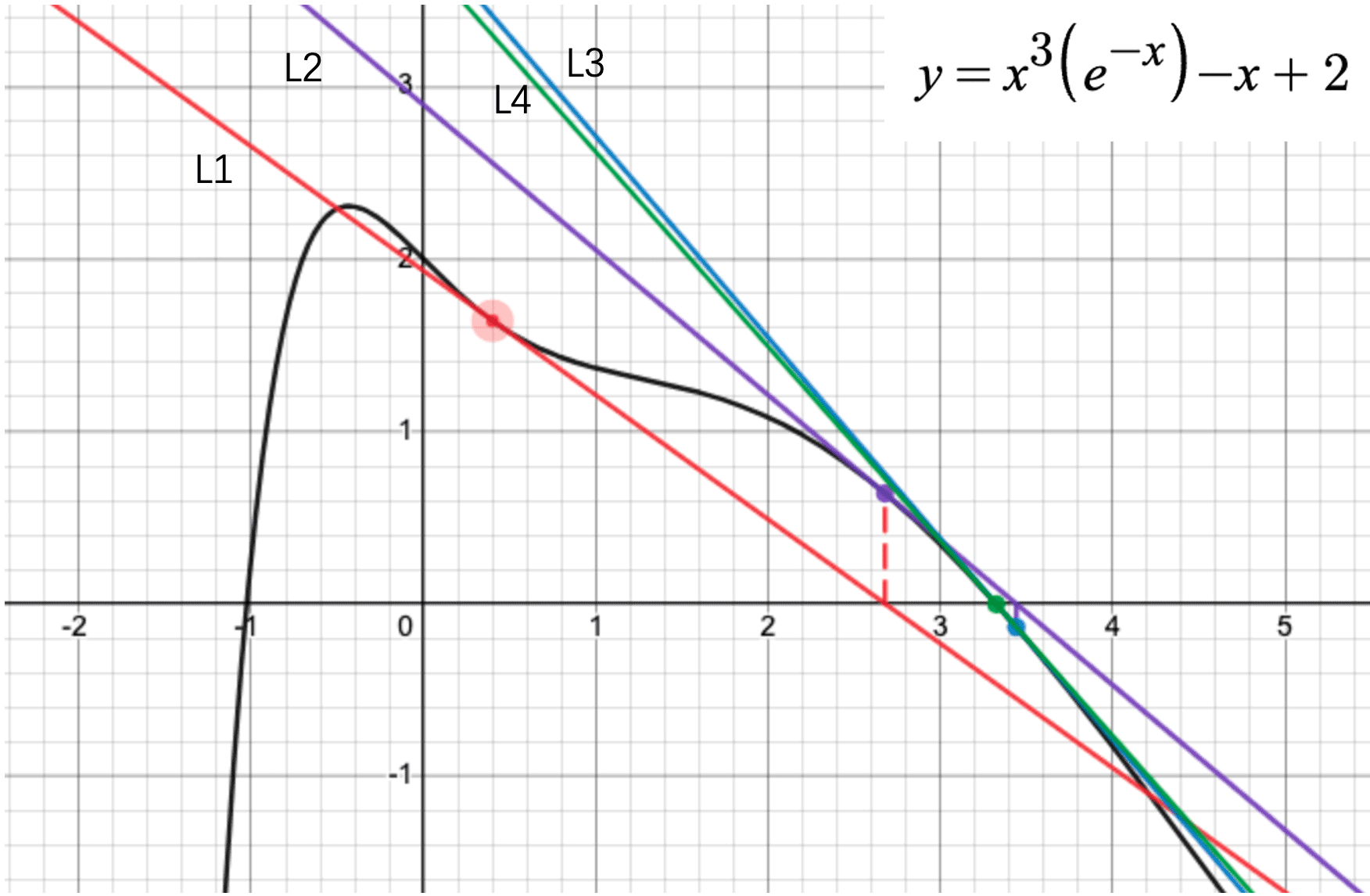贝塞尔曲线有广泛的用途,如动画曲线、字体设计、建模等,如下图所示。
在设计领域广泛使用的曲线为三次贝塞尔曲线。
起源介绍
为什么要使用曲线?
如何把纸上书写的文字、绘制的图案在计算机中显示和存储? 最简单的方法是用像素点来表示,也就是拍照的方式。但这种方法无法矢量化,例如无法表示大小不同的文字和茶壶,并且此种方法占用的存储空间大,且边缘可能会不平滑。
因此,早期的人们就想到了使用曲线来拟合纸上的图案或者现实世界中的物体。
为什么是三次曲线?
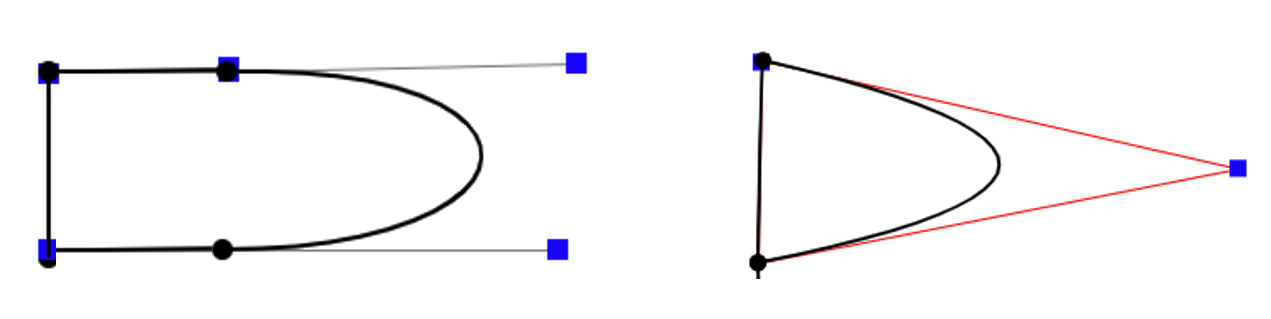
曲线又分为一次曲线、二次曲线、三次曲线、四次曲线等。如果我们想要两条不同的曲线的连接点能够光滑的话,那么至少需要三次曲线。如下图所示,左图为三次贝塞尔曲线,右图为二次贝塞尔曲线。
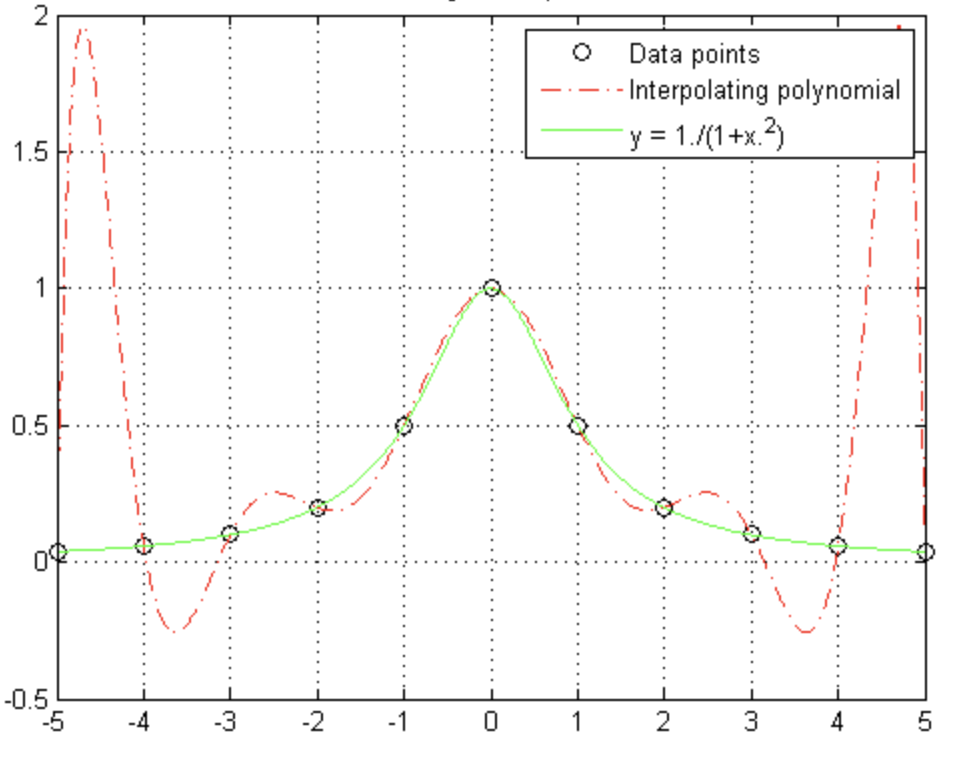
比三次高的曲线则容易出现抖动,可能无法反映实际物体的形状规律。如
下图所示:
图中的圆圈表示原始的数据,绿色曲线为低次的拟合曲线,红色曲线为高次的拟合曲线。高次曲线容易出现频繁抖动,可能无法反映原始数据的规律和趋势,且计算量会比较大。 因此,三次曲线是一个刚好合适的曲线。
为什么是贝塞尔?
三次曲线的一般形式为:
y = a*x^3 + b*x^2 + c*x + d
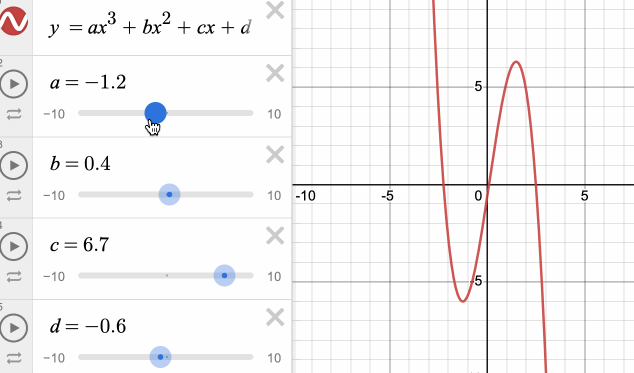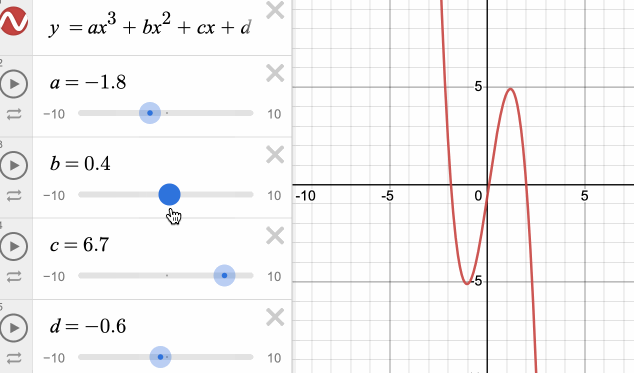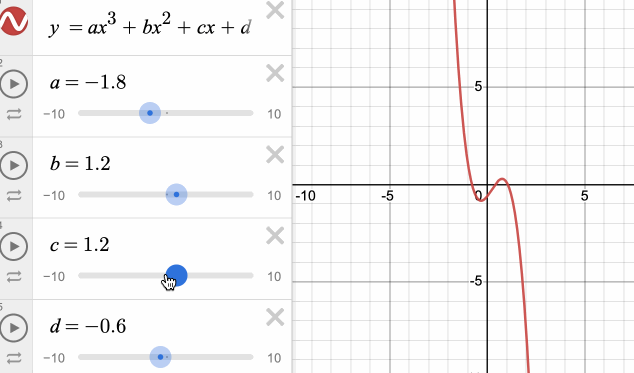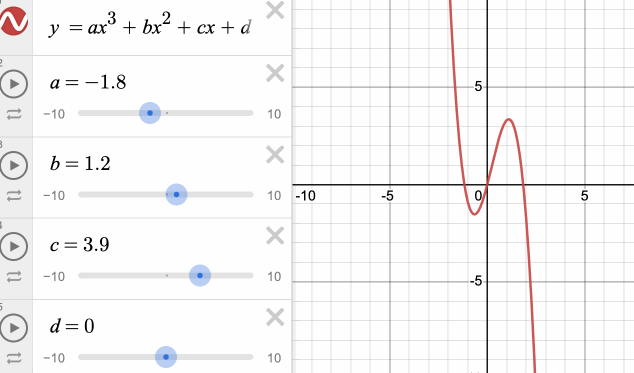
该方程共有4个控制变量。分别修改这4个变量对曲线的形状的影响如下图所示:
我们发现,修改这几个参数对曲线的影响并不是很直观,且很难快速地拟合出想要的形状。另外,常见曲线的表示形式还有圆、椭圆、双曲线的标准方程,它们的参数虽然具备实际的意义,但又不够通用。
除了要达到方便拟合形状的目的外,还需要具备让多条曲线之间容易光滑连接的特性。贝塞尔曲线正是为了解决这些问题而诞生的。
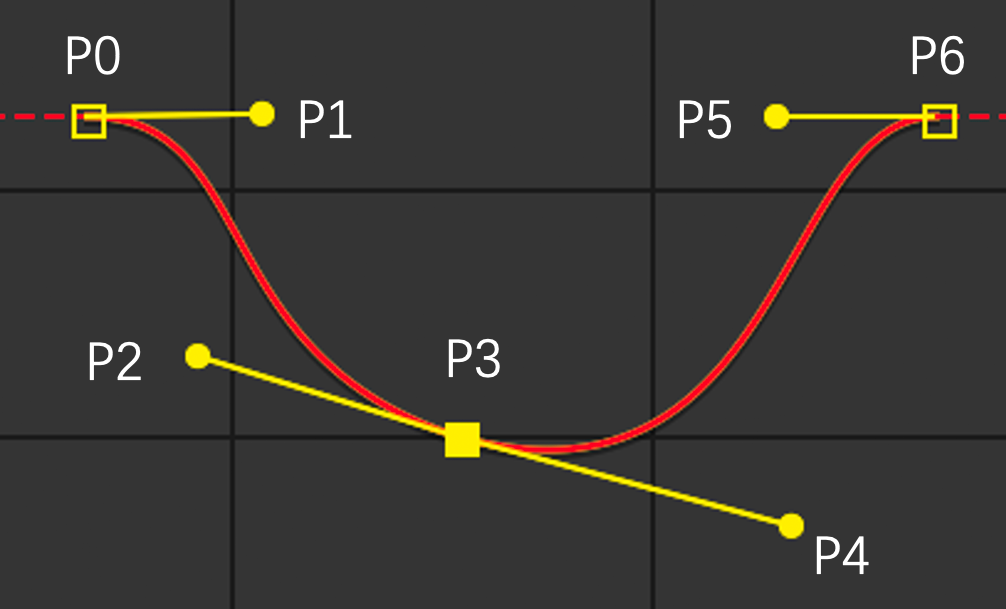
贝塞尔曲线由若干个控制点定义,包括曲线上的点以及曲线外的点,如下图所示:
图中的曲线共有7个控制点,包括3个在曲线上的点。曲线上的点在两个终端的位置上各有一个在曲线外的控制点;在非终端位置上,则各有两个在曲线外的点,相互之间连成了两条控制线,如图中的LP2P3与LP3P4。
准确地说,该条曲线是由两条贝塞尔曲线组成,每条三阶贝塞尔曲线都有4个控制点。由于这两条曲线共用了P3点,所以总共有7个控制点。当两条曲线在P3点的位置斜率一样时,两条曲线连接光滑。
我们可以很方便的通过控制线修改曲线的形状。从直观上来说,控制线的斜率,决定了曲线在控制点位置的方向;控制线的长度,决定了曲线贴合控制线的程度。
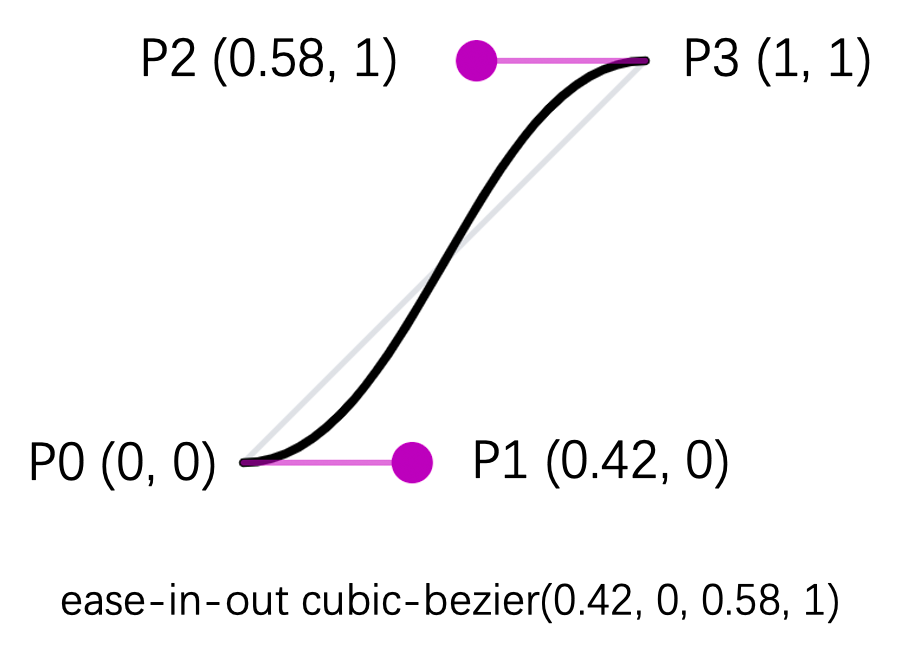
CSS的cubic-bezier同样也是有四个控制点:
不一样的是,起点与终点始终固定为(0, 0)、(1, 1),另外两个控制点由CSS的cubic-bezier(x1, y1, x2, y2)属性控制,如图中的P1、P2。
CSS贝塞尔曲线的y坐标是一个相对单位,范围为[0, 1]。实际设定的属性值是在具体的CSS属性如transform中设定的,使用这个相对值结合实际的起始与终始值,就可以换算成真实的值,举例如下:
translateX = translateXBegin + (translateXEnd – translateXBegin) * y + translateXBegin
假设我们需要让同一个元素的同一个属性的两段连续的CSS动画之间的变化保持光滑变化的话,那么我们需要保证第二段动画起点控制线的斜率与第一段动画终点控制线的斜率保持一致。例如,ease-in-out控制线的斜率为0,若两段动画都为ease-in-out,那么这两段动画的连接位置是光滑的。
贝塞尔曲线是曲线的一种参数化形式。
参数化曲线
参数化曲线引入了一个参数变量t,分别表示x、y:
x(t) = f(t)
y(t) = g(t)
举一个简单的例子,定义如下曲线方程:
x(t) = 1 – t
y(t) = 2t^2 + 1
该曲线的形状如下图所示:
通过x(t)方程求解t,可得到该曲线的一般方程为:
y = 2x^2 + 4x – 1
然而,并非所有的参数化曲线都可以简单地表示为一般方程,如:
x(t)是一个三次方程,三次方程有三个根,且可能会存在复根。将x(t)的根代入y(t)方程上,需要区分若干种情况。情况就会变得复杂。由此,参数化方程的一个重要意义是可以表示一般方程难以甚至无法表示的形式。
N阶贝塞尔曲线
一阶贝塞尔曲线
一阶贝塞尔曲线的方程为:
x(t) = c0 + t(c1 – c0)
y(t) = v0 + t(v1 – v0)
其中,c0, v0, c1, v1为常量,若使用点P0(c0, v0)、P1(c1, v1)表示这四个常量,则一阶贝塞尔曲线的方程为:
B(t) = P0 + t(P1 – P0) = tP1 + (1 – t)P0
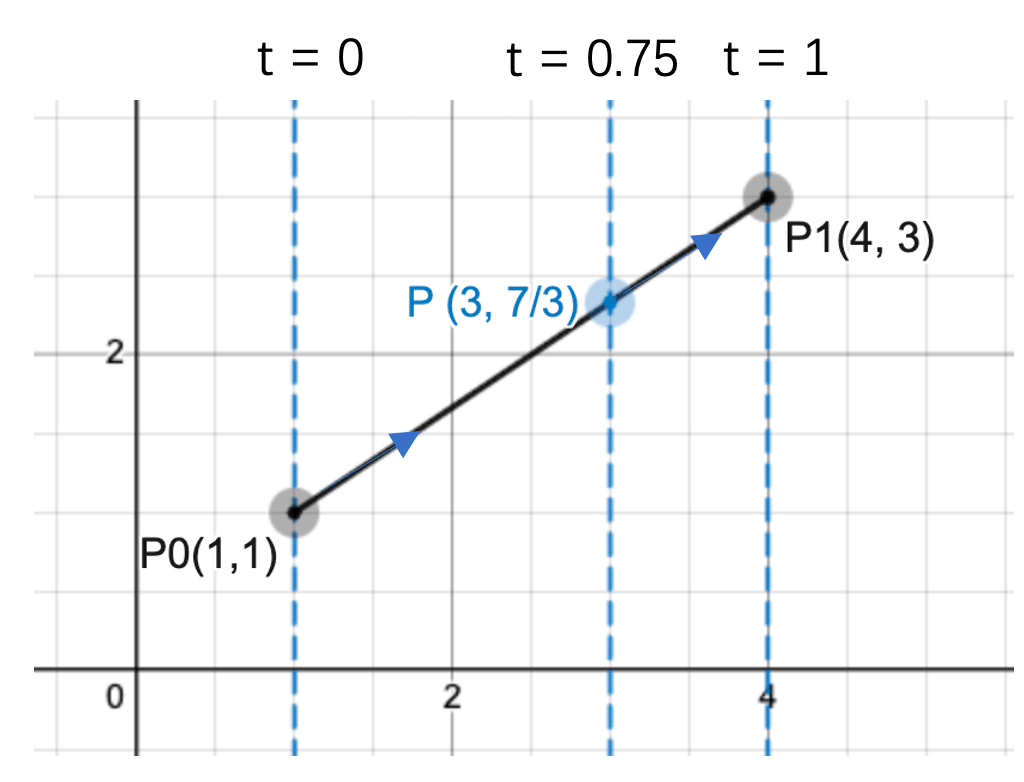
通过x(t)求解t再代入y(t),可知一阶贝塞尔曲线为一条直线。取P0(1, 1),P1(4, 3),则曲线的形状如下图所示:
如图所示,现在根据t求解曲线上的点:
(1)当t = 0时,求解可知曲线上的点为(1, 1);。
(2)当t = 0.25时,曲线上的点为(3, 7/3)。
(3)当t = 1时,曲线上的点为(4, 3)。
可观察到,一次贝塞尔曲线可直接通过线性插值求解。也就是说,t值与x值的变化速率是相等的(方向可能会相反)。
二阶贝塞尔曲线
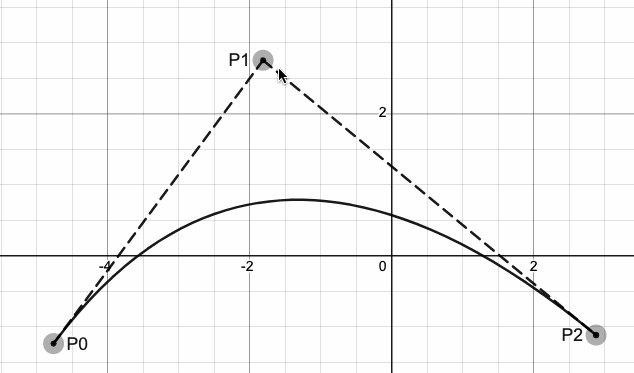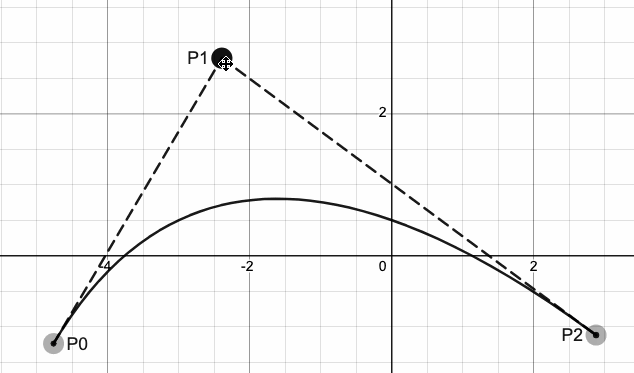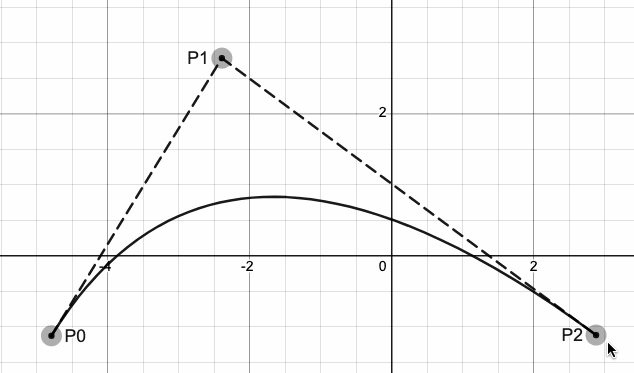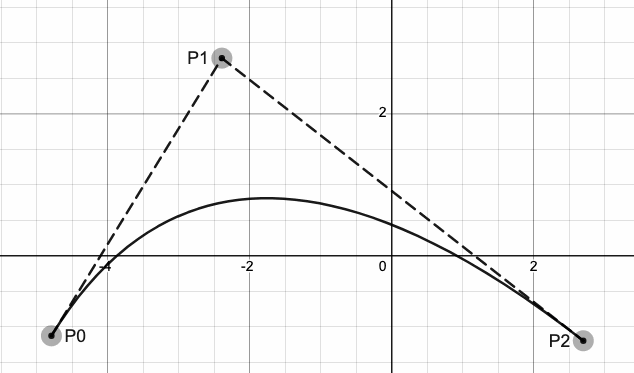
二阶贝塞尔曲线的方程及形状如下图所示:
二阶比一阶多了一个控制点。通过修改控制点的位置可改变曲线的形状:
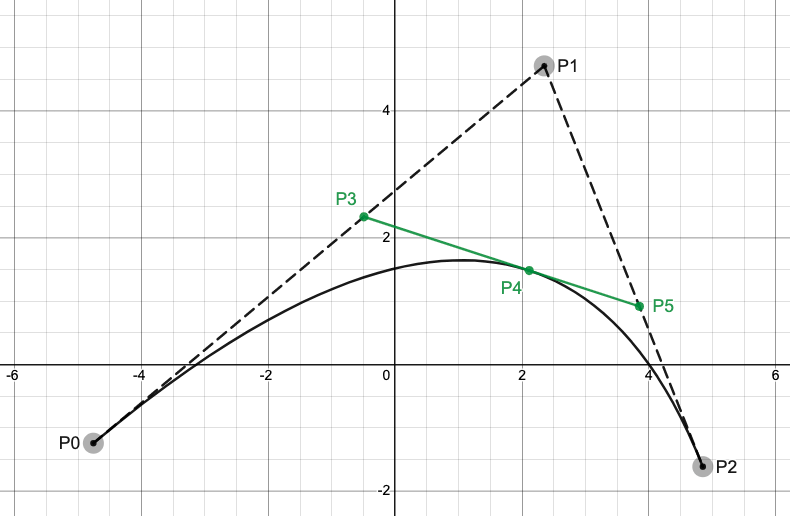
根据t求解二贝塞尔曲线,可按如下步骤:
(1)将线段LP0P1当作一阶贝塞尔曲线,根据t求解该曲线上的点为P3。
(2)将线段LP1P2当作一阶贝塞尔曲线,根据t求解该曲线上的点为P5。
(3)将线段LP3P4当作一阶贝塞尔曲线,根据t求解该曲线上的点为P4。P4即为二阶贝塞尔曲线上的点。
如下图所示,图中t = 0.6,求解后的点为P4.
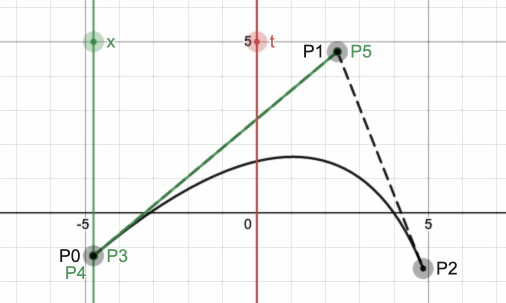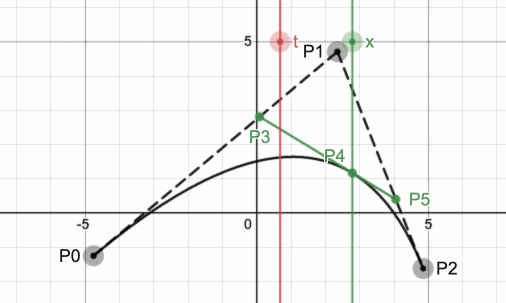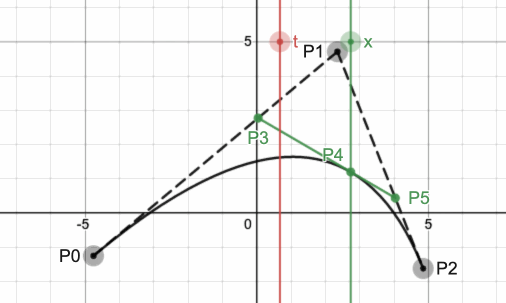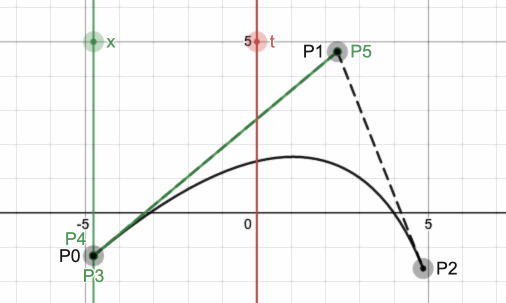
当t从0到1之间变化时,曲线上的点变化如下所示:
可见,在二阶曲线上,t值与x值的变化速率不是同步的。在动画曲线场景,x值表示时间,y值表示作动画的属性如translate,而t值只是一个没有具体意义的参数变量,范围为[0, 1]。此处需要注意,t值不是表示时间。
上面我们将求解二阶贝塞尔曲线转化成了求解三个一阶贝塞尔曲线。这在数学上是可以
证明的。
定义一阶曲线的方程为lerp函数:
lerp(P0, P1, t) = tP1 + (1 – t)P0
已知P0,P1,P2点,根据该方程求解两条一阶贝塞尔曲线的解P3、P5为:
P3 = lerp(P0, P1, t) = tP1 + (1 – t)P0
P5 = lerp(P1, P2, t) = tP2+ (1 – t)P1
然后,同样套用lerp函数,求由P3、P5定义的一阶贝塞尔曲线的解,即由相同的t值决定的P4点:
P4 = lerp(P3, P5, t) = (1 – t)^2 P0 + 2t(1 – t)P1 + t^2 P2
求解P4点所用的该方程即为二阶贝塞尔曲线的方程。这里体现了贝塞尔曲线的一个精妙之处。
三阶贝塞尔曲线
三阶贝塞尔曲线比二阶曲线增加了一个控制点,它的方程与形状如下图所示:
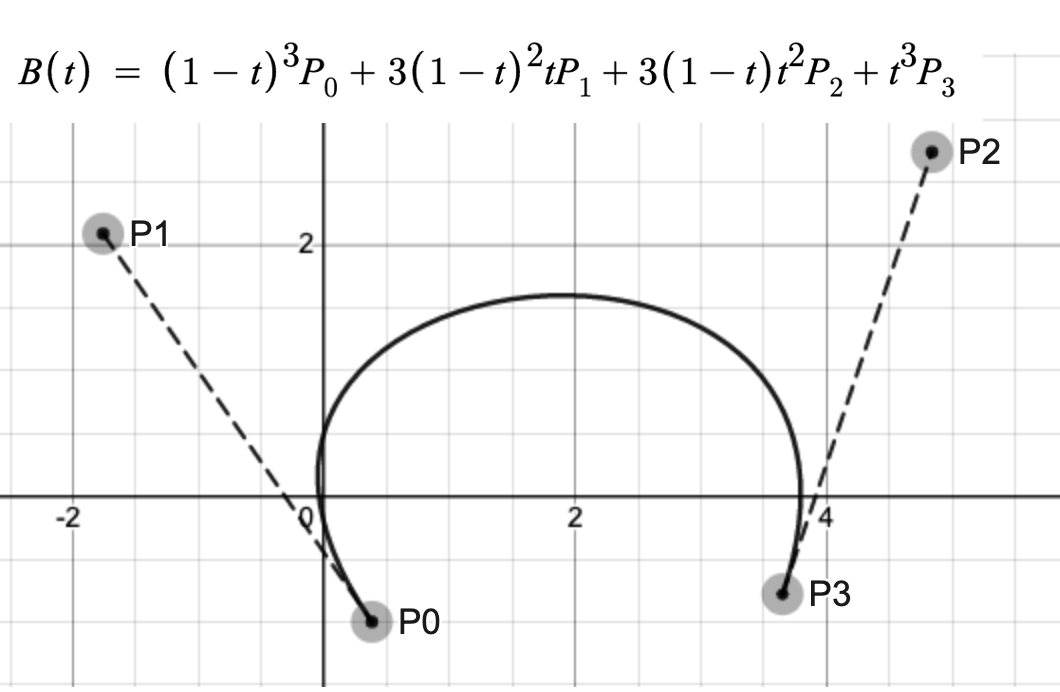
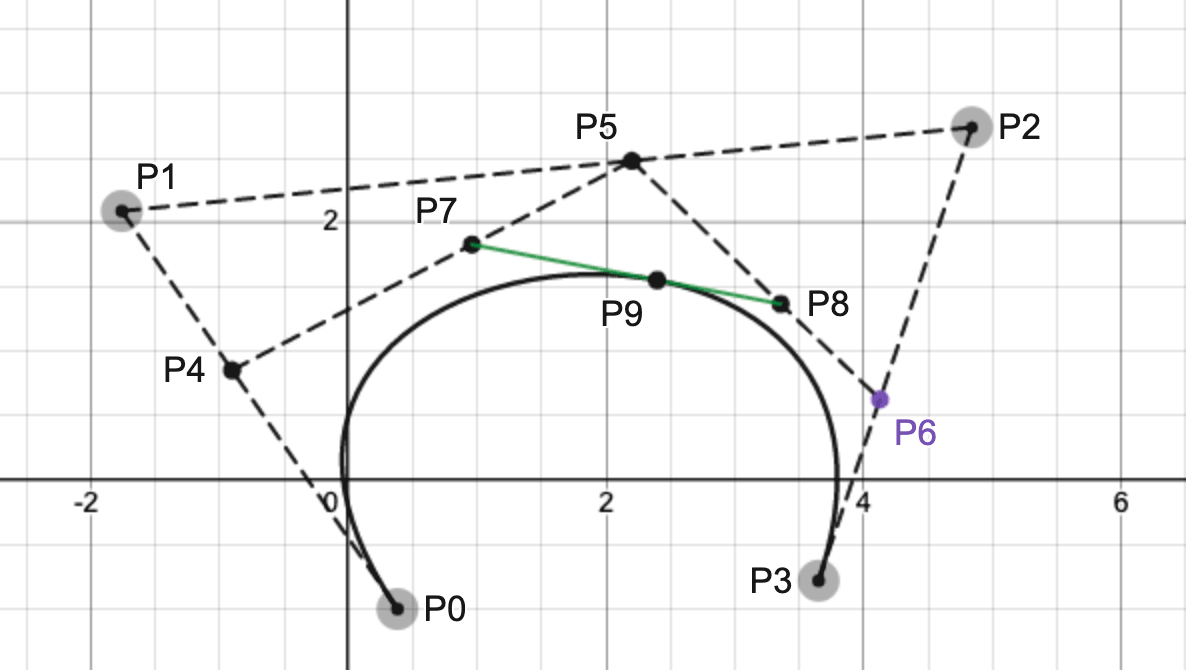
求解三阶贝塞尔曲线可以使用与求解二阶贝塞尔曲线类似的方式,如下图所示(t = 0.6):
将P1与P2连接,然后在三条线段上(LP1P0、Lp1P2、LP2P3)分别求解一阶贝塞尔曲线的值,得到P4、P5与P6点。此时三阶曲线降为二阶曲线。再用同样的方式得到P7与P8点,将求解二阶贝塞尔降为求解一阶贝塞尔曲线,得到曲线上的点P9.
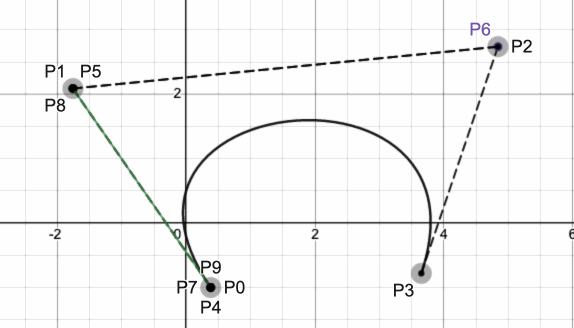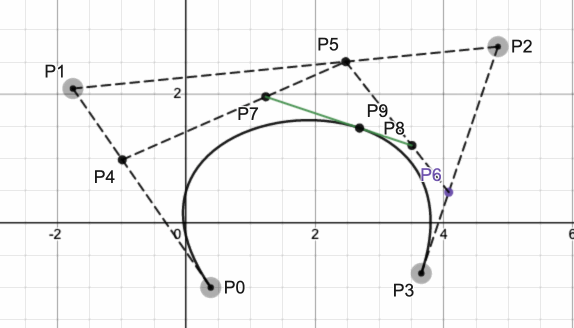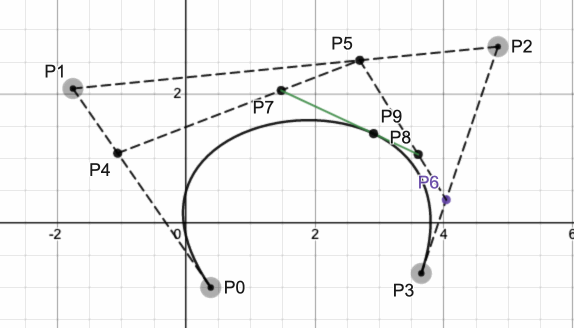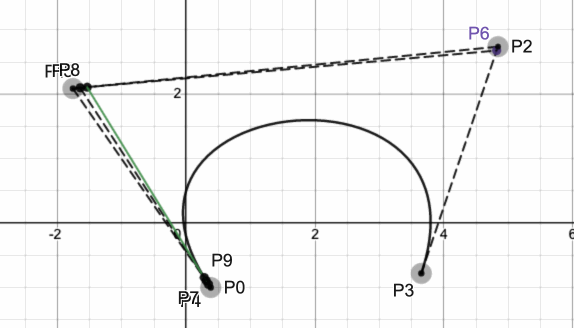
当t从0到1之间变化时,曲线上的点变化如下所示:
同样也可以通过套用lerp函数得到证明。可见,多阶贝塞尔曲线是一种递归的定义。更高阶的贝塞尔曲线,如四阶、五阶,同样可以通过类似的方式进行定义、绘制、求解。
动画贝塞尔曲线
如前文所说,通常动画贝塞尔曲线的x值表示时间,且是一个范围为[0,1]相对单位;y值表示作动画的属性,在CSS动画中y值也是一个[0, 1]的相对单位;而t值作为参数变量,不代表实际的意义。
动画使用的贝塞尔曲线要求曲线是单值函数,即一个x值只能对应一个y值,而不能是多值函数。两者对比如下图所示:
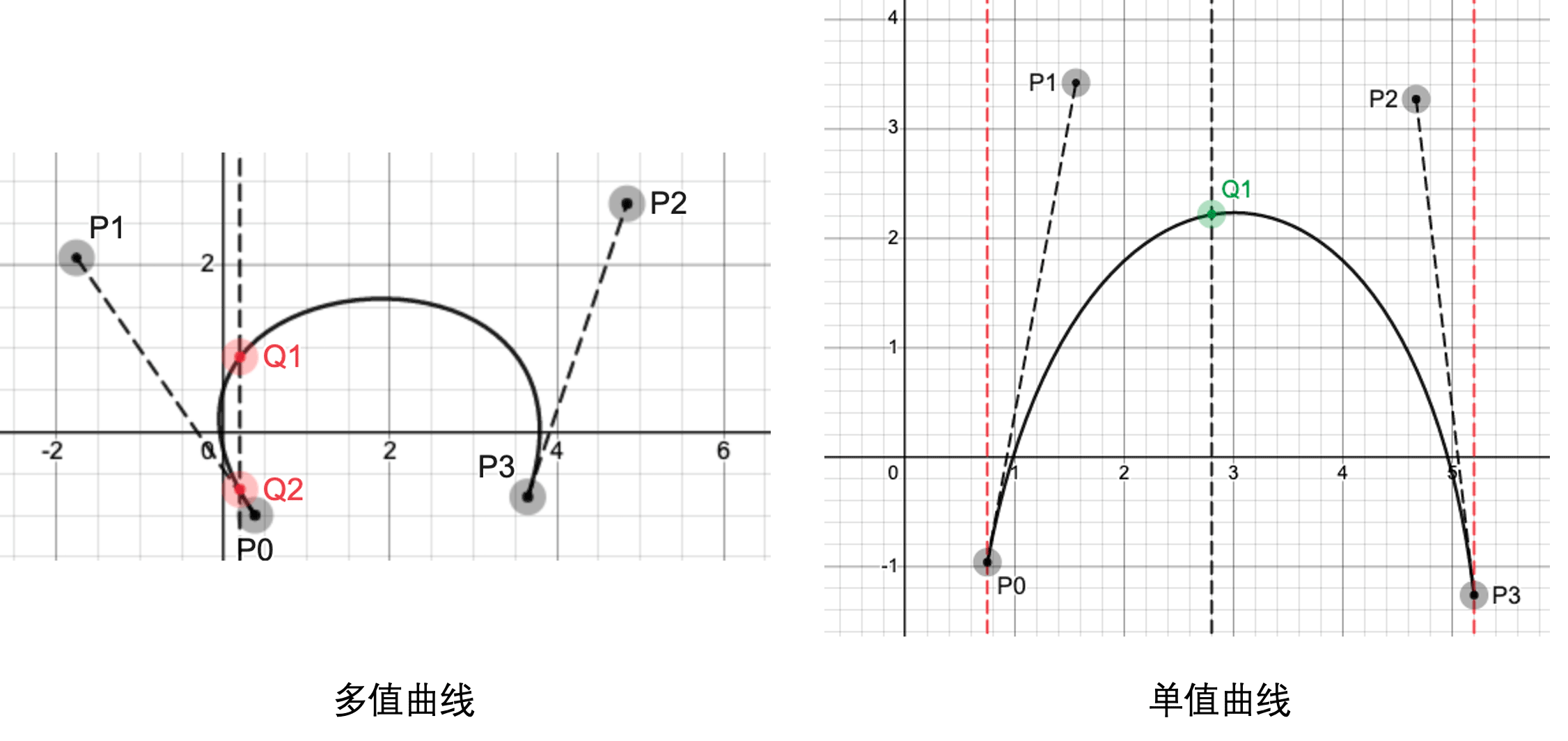
这里要求P1的x坐标不能小于P0的x坐标,P2的x坐标不能大于P3的x坐标。
动画贝塞尔曲线值求解
前文已经演示了使用降阶的方式求解贝塞尔曲线。该方式存在一定的计算量,其他求解方式还有以下几种。
求解三次方程的根
由于t不是时间,所以无法直接使用时间计算。需要根据x(t)的方程,求解t,然后再代入y(t)的方程。该方法的计算量也是比较大的,套用三次方程的根的方程的计算量比较大。
使用简单的曲线拟合
该方法对常用的一些曲线如ease-in-out,使用其他的曲线进行拟合。这种曲线为一般形式的方程,不存在变量t。如下代码所示:
|
|
function easeInOutCubic(x: number): number { return x < 0.5 ? 4 * x * x * x : 1 - pow(-2 * x + 2, 3) / 2; } |
ease-in-out拟合的效果与真实的曲线对比如下:
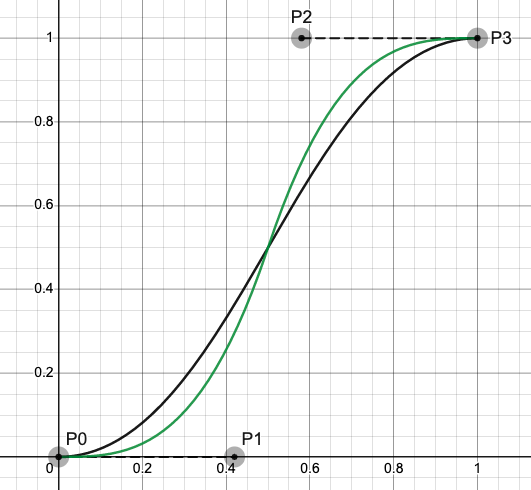
其中绿色的线为拟合曲线。我们发现,两者差别挺大的。对还原度要求高的场景不推荐使用该方式。
使用二分逼近的方式求解
二分逼近的实现如下代码所示:
|
|
while (t0 < t1){ x2 = curveX(t2); if (Math.abs(x2 - x) < epsilon) return curveY(t2); if (x > x2) t0 = t2; else t1 = t2; t2 = (t1 - t0) * .5 + t0; } |
通过二分t值,去逼近时间x,当计算得到的x(t)值与实际传参的x值的差值小于容忍的误差后,则将使用此t去求解y值。
推荐的时间误差计算方式为:
|
|
// epsilon determines the precision of the solved values // a good approximation is: var duration = 10000; // duration of animation in milliseconds. var epsilon = (1000 / 60 / duration) / 4; |
如一个10s的动画,推荐误差为0.0004,换算后为4ms。此方式计算速度较快,且满足精度要求。
牛顿迭代法
牛顿迭代法是一种求解方程根的重要方式,举例说明,如下图所示:
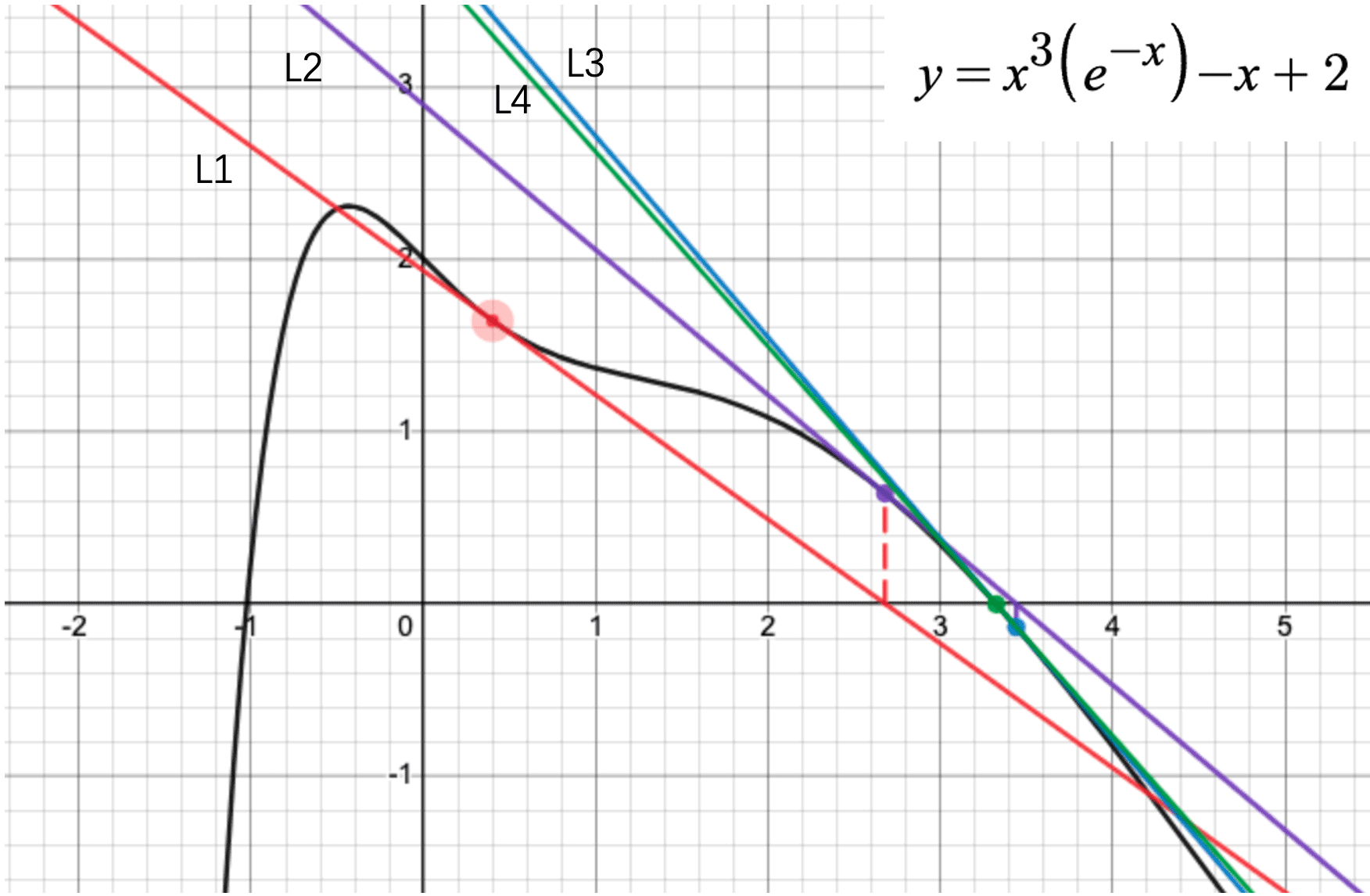
为了求解图中所示方程的y = 0的解。按以下步骤进行:
(1)任意选取一个起始点,如图中的x1 = 0.4,计算y1 = f(x1)的值,该值与0相差较大,因此x = 0.4不是方程的解。
(2)作曲线在(x1, y1)上的切线L1,与x轴相交于点(x2, 0)。
(3)计算y2 = f(x2),同样该值与0相差较大,也不是方程的解。
(4)作曲线在(x2, y2)上的切线L2,与x轴相交于点(x3, 0)。
(5)按同样的步骤得到切线L3与L4,由图可见f(x4)的值已经非常接近0(绿色的线与曲线的交点).
通过观察可知,图中4个切线逐渐收敛到y = 0的位置。
求解贝塞尔曲线的x(t)方程也是同样的方式:
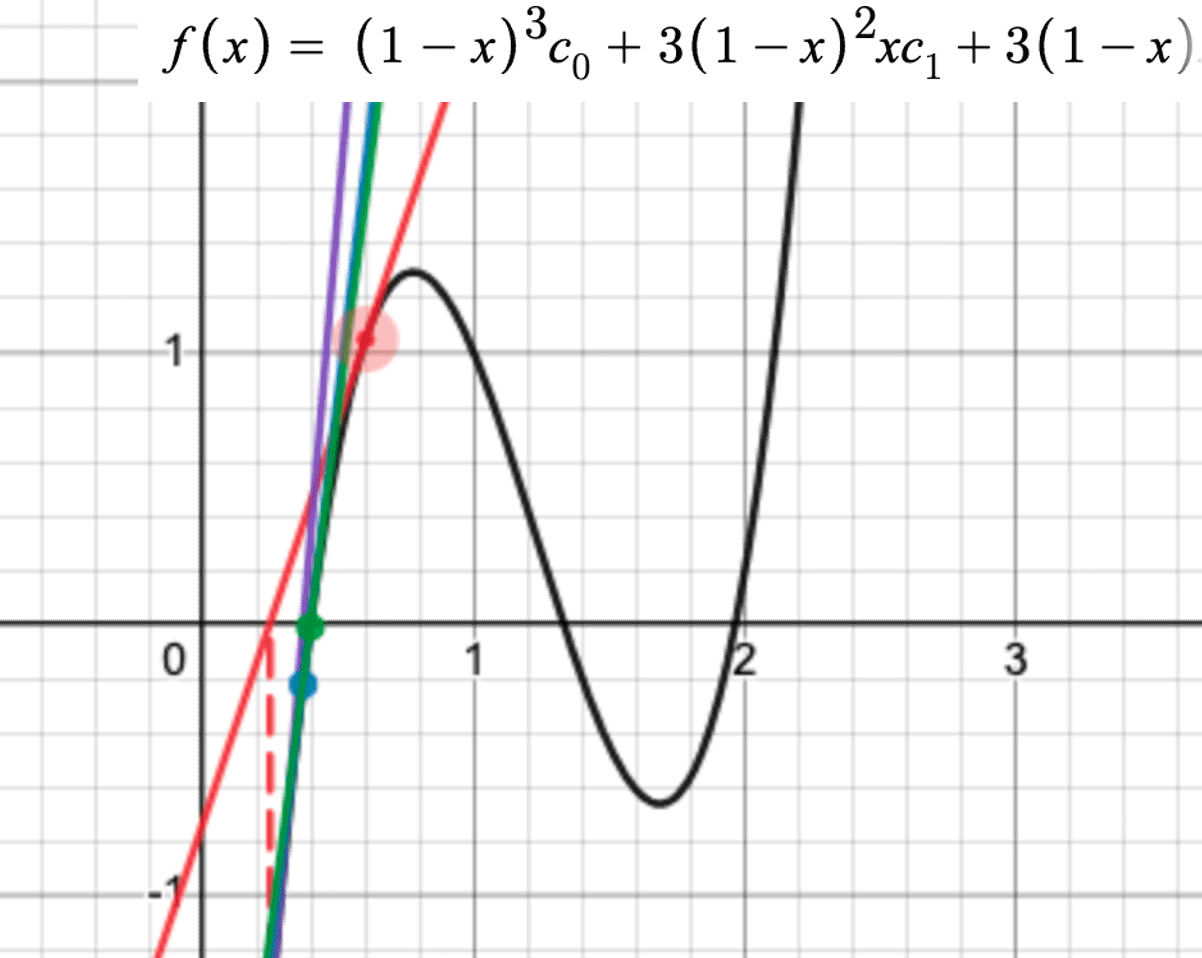
第四条绿色的切线与曲线的交点,同样也接近x(t)= 0位置。
若计算所求的x(t)值不为0,则需要在计算过程中减去,如下代码如下所示:
|
|
// First try a few iterations of Newton's method -- normally very fast. for (t2 = x, i = 0; i < 8; i++){ x2 = curveX(t2) - x; if (Math.abs(x2) < epsilon) return curveY(t2); // 误差值在容忍范围内 d2 = derivativeCurveX(t2); if (Math.abs(d2) < 1e-6) break; // 出现导数为0的情况时退出循环 t2 = t2 - x2 / d2; } t0 = 0, t1 = 1, t2 = x; if (t2 < t0) return curveY(t0); if (t2 > t1) return curveY(t1); // Fallback to the bisection method for reliability. // 牛顿迭代没有收敛时,使用二分逼近法,代码同上所示,略 |
由于牛顿迭代法需要满足一定条件才会收敛,可能会出现不收敛的情况,此时需要降级到上面的二分法。牛顿迭代法比二分法快很多,因此优先使用该方法求解。
这个方法被bezier-easing这个npm库与Chromium所使用。我们发现两者甚至连注释都是一样的,详见bezier_curve.cc文件。
综上,贝塞尔曲线使用参数化的形式表示它的方程,达到了灵活控制曲线形状的目的,同时也给求解方程造成了一定的麻烦。在计算机软件中的求解,通常使用牛顿迭代法结合二分逼近法的方式。
Post Views:
3,510