在JavaScript里面产生随机数的方式是调用Math.random,这个函数返回[0, 1)之间的数字,如:

如果想要产生整数的随机数,那么只需要稍微换算一下,例如产生[10, 20]之间的整数,那么可通过以下代码即可:
|
1 |
Math.floor(Math.random() * 11) + 10 |
如何实现一个自定义的random的函数呢,即怎么实现一个随机数发生器(RNG,Random Number Generator),一个比较简单的实现如下代码所示:
|
1 2 3 4 5 6 |
// from stackoverflow var seed = 1; function random() { var x = Math.sin(seed++) * 10000; return x - Math.floor(x); } |
如上代码,这个函数需要一个种子seed,每次调用random函数的时候种子都会发生变化。在控制台进行实验:
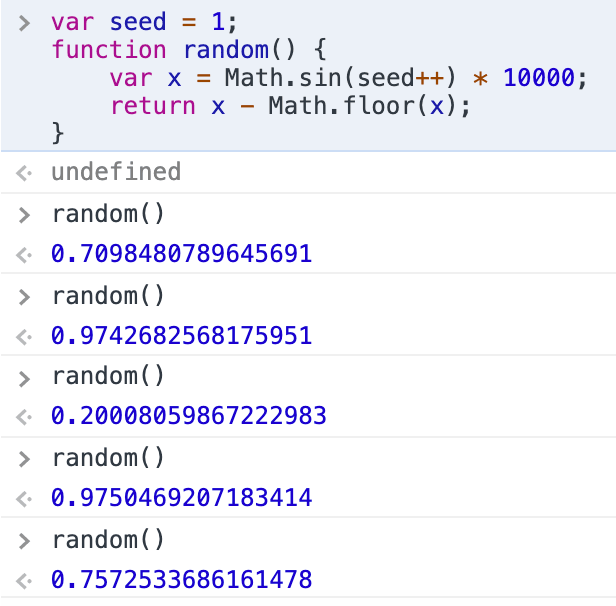
可以看到,结果还是挺随机的。为什么随机数发生器需要一个种子呢?因为对于一个没有输入的函数,不管执行多少次,其运行结果都是一样的,所以需要有一个不断变化的入参,这个入参就叫种子,每运行一次种子就会发生一次变化。
那么我们直接用Math.random不就好了吗,为什么还要自己实现一个random函数呢?有一些场景需要我们能控制随机数的产生,例如在在线大转盘场景里面,转盘的转动是随机的,但是各方需要保持一样的随机,所以如果各方都使用相同的随机函数,就能够保证各方产生的随机序列是一样的,如下图所示:
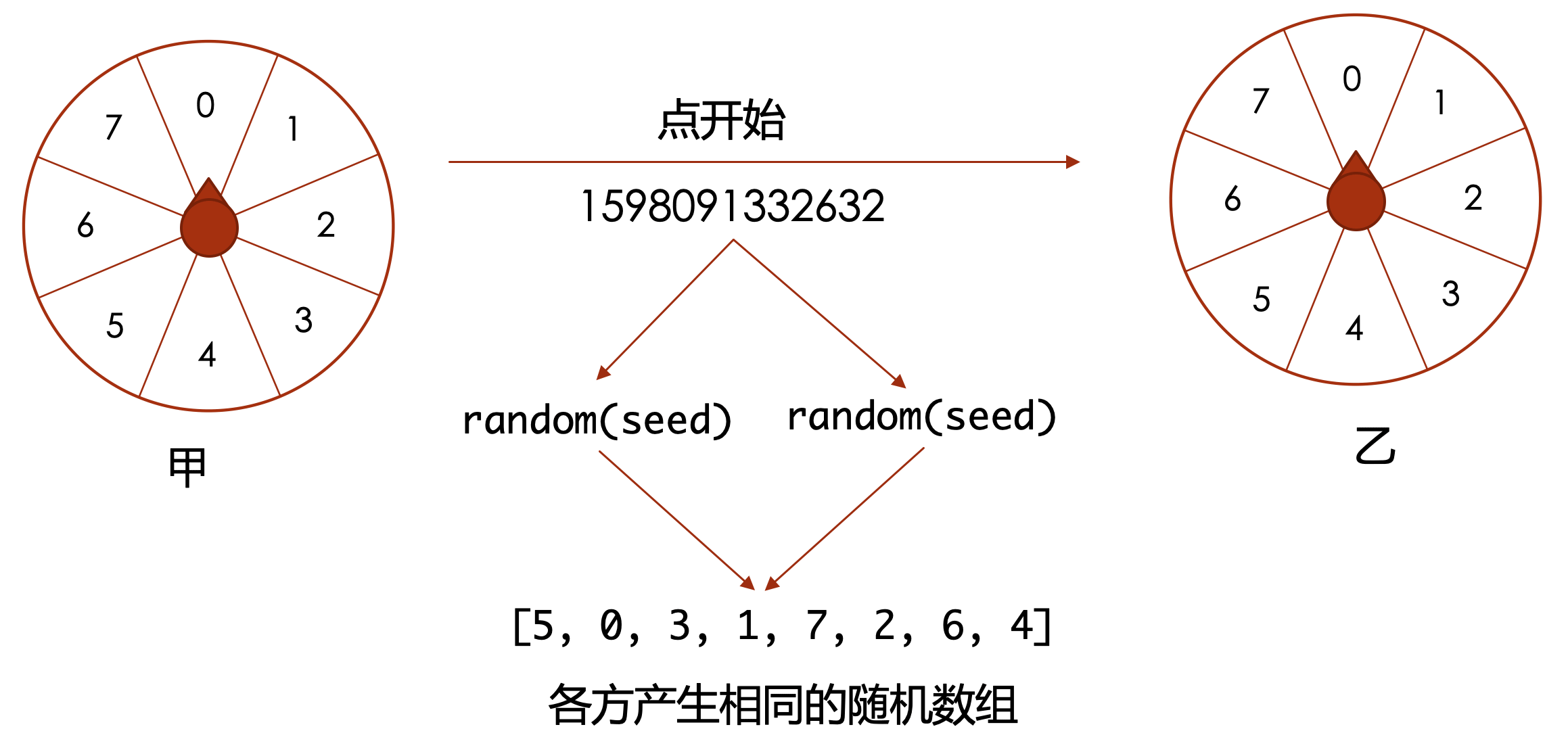
甲触发开始之后,通知其他各方,并带上一个当前的时间戳,所有人使用这个时间戳做为随机种子,并使用相同的随机数函数,那么就能保证所有人产生的随机序列是一样的。
然后我们再来看一下C库里面的rand函数,这个函数返回[0, RAND_MAX)之间的整数( RAND_MAX 根据实现, 最小值 >= 32767 ),如下代码所示:
|
1 2 3 4 5 6 7 |
/* 初始化随机数发生器,使用当前时间戳(秒)*/ srand((unsigned) time(&t)); /* 输出 0 到 49 之间的 5 个随机数 */ for( i = 0 ; i < n ; i++ ) { printf("%d\n", rand() % 50); } |
上面代码先调用srand设置随机种子,使用的种子是调用time函数返回的时间戳,单位为秒,然后再调用rand函数生成随机数。可以发现,这个函数存在一个明显缺陷:当你在同一秒内运行该程序,产出的随机数将会是一样的。
C库的rand函数实现非常简单,如下代码所示:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
static unsigned long int next = 1; // 初始种子为1 int rand(void) // RAND_MAX assumed to be 32767 { next = next * 1103515245 + 12345; return (unsigned int)(next / 65536) % 32768; } void srand(unsigned int seed) { next = seed; } |
代码第一行的next便表示种子,而随机数是通过简单的四则运算得到的,效率会比我们上面的使用的求解正弦会更高一些。
那么为什么JavaScript的Math.random不需要种子呢,它是怎么实现的呢?ES5对Math.random的规定是这样的:
15.8.2.14 random ( )
Returns a Number value with positive sign, greater than or equal to 0 but less than 1, chosen randomly or pseudo randomly with approximately uniform distribution over that range, using an implementation-dependent algorithm or strategy. This function takes no arguments.
翻译一下就是,产生的值是在[0, 1)之间,并且具有大致的均匀分布,不用带参数。
我们可以看一下V8里面是怎么实现Math.random的,它的实现代码是在math-random.cc和math.tq这两个文件,实现逻辑如下代码所示:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
// 取出当前随机数的状态 State state = native_context.math_random_state(); // 如果cache还没初始化,那么进行初始化 if (state.s0 == 0 && state.s1 == 0) { uint64_t seed; // 产出一个随机种子 random_number_generator()->NextBytes(&seed, sizeof(seed)); // 把种子进行哈希散射生成另两个数s0和s1 state.s0 = base::RandomNumberGenerator::MurmurHash3(seed); state.s1 = base::RandomNumberGenerator::MurmurHash3(~seed); } // 取出cache FixedDoubleArray cache = native_context.math_random_cache(); // Create random numbers. for (int i = 0; i < kCacheSize; i++) { // kCacheSize = 128; // Generate random numbers using xorshift128+. // 使用s0和s1进行一些位移运算得到一个随机数(s0) base::RandomNumberGenerator::XorShift128(&state.s0, &state.s1); // 把整数的随机数转成小数,并存到cache里面 cache.set(i, base::RandomNumberGenerator::ToDouble(state.s0)); } |
具体过程如上注释所示,每次会一次性产生128个随机数,并放到cache里面,供后续使用。我们比较关心的是代码第7行的随机种子是怎么产生的。经过打断点调试,我们发现最后是调用RandBytes函数,这个函数是通过读取/dev/urandom文件的8个字节得到一个随机数。urandom是Linux系的系统上源源不断产生随机数据的特殊文件。而在Windows系统上则会调用rand_s函数,rand_s是Windows系统提供的一个随机性足够强的随机数发生器。而在其他系统则是通过获取当前系统高精度的时间戳。所以我们看到Chromium随机数的源头是借助了操作系统的能力。
我们可以把cache里面的128个数字打印出来,并和控制台的运行结果进行对比,如下图所示:
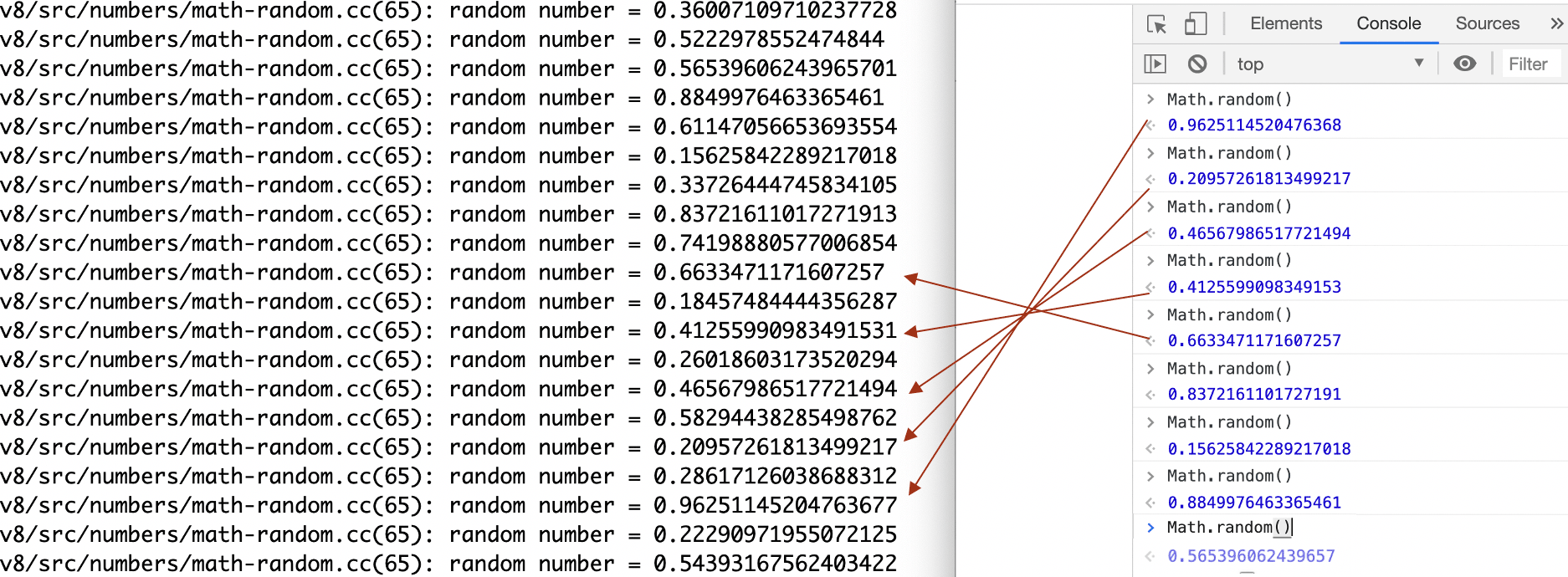
打印的结果是从后往前取的,如果index为0,说明随机数用完了,需要重新生成一批随机数。这里我们也看到,在Chrome控制台未执行Math.random之前,我们已经能够预测到下一个随机数是什么了。所以这里的随机数具有可预测性,这种由算法生成的随机数也叫伪随机数。只要种子确定,随机算法也确定,便能知道下一个随机数是什么。
当我们查阅MDN文档的时候,文档上说Math.random是不安全的,不能够做为安全用途,如加密,如下图所示:

需要使用window.crypto.getRandomValue函数。为什么说Math.random是不安全的呢?从V8的源码可以看到Math.random的种子来源是/dev/random,取64位,种子的可能个数为2 ^ 64 随机算法相对简单,只是保证尽可能的随机分布。
通过查阅一些资料我们发现window.crypto.getRandomValue的实现在Safari,Chrome和Opera浏览器上是使用带有1024位种子的ARC4流密码。你可能会说 2 ^ 64难道还不够大吗?我们知道扑克牌有52张,总共有52 ! = 2 ^ 226种组合,如果随机种子只有2 ^ 64种可能,那么可能会有大量的组合无法出现。
当随机数种子范围较少或者是算法不够优,在多次取值之后可能会出现周期性,有人做了个实验,如下图所示:

左图是PHP的rand函数在Windows上的结果,右图是通过一个高质量的随机数发生器产生的结果。这个实验通过不断产生随机色值,然后打点,就得到以上结果。可以看到,左图出现了一些规律性的花纹,而右图则是无规律的噪点。
接着,我们再说一下随机数的一个应用:洗牌算法——给定一个数组如[1, 2, 3, 4, 5, 6],处理为一个随机排列的数组如输出为[3, 1, 6, 2, 5, 4]。一个标准解法如下代码所示:
|
1 2 3 4 5 6 |
function shuffle(arr) { for (let i = 0; i < arr.length; i++) { let j = i + Math.random() * (arr.length - i) >> 0; swap(arr, i, j) } } |
原理是每次都和当前及后面的数之中随机选中一个进行交换,如1可以和1, 2, …, 6任选一个进行交换,而当第一个位置确定好了之后就不再动它了,所以2是和2及之后的数字进行交换。在控制台实验这个算法的效果,如下图所示:

可以看到,每次运行都能够产生一个随机排列的数组。这也正是上面提到的大转盘所使用的方法。
然后我们再来看一个不好的案例:《当随机不够随机:一个在线扑克游戏的教训》,这个案例说的是1999年的时候一个很流行的在线扑克网站公布了他们所使用的洗牌算法,如下图所示:

它使用的语言是Pascal,逻辑实现和我们上面的标准解法类似,但是有一些明显的bug。原文里面列了几个,这里我们也讨论一下:
(1)差1错误——因为random函数返回的值是[0, 50],所以导致第52张牌永远无法停留在第52个的位置
(2)洗牌不均匀——这个算法可能会把之前已经换好的牌重新调换顺序,越往前排的位置得到的换牌机会会更多。
(3)使用32位的种子——种子的可能性总共只用2 ^ 32个,相对于52!差很多。
(4)使用ms的系统时间做为种子——这里使用的是从当天午夜零点到当前的ms数,而一天总共只有86,400,000ms,所以产生的随机数总共只有这么多种可能,如果黑客将系统时间和服务的时间进行同步到秒级,那么便可把可能性降低到1000种,然后再根据已知的牌进行检索便可准确知道所使用的随机种子是哪一个。
做为一个生产环境的应用,这样的实现是有明显漏洞的。
和伪随机数(Pseudo Random Number )相对的是真随机数(True Random Number ),真随机数需要从现实世界进行采集。上文所说的/dev/urandom是生产伪随机数的一个文件,而/dev/random则是生产真随机数的文件,/dev/random的一种实现是通过设备驱动程序采集背景噪音。有一个提供真随机数的网站叫random.org:

它是通过采集大气噪音生成的随机数,你可以使用它提供的免费接口做为你的随机数来源。
今年还有厂商推出了量子随机数手机,查阅了一下:
工作原理是:LED发出随机数的光子,CMOS捕获光源散粒噪声产生随机序列,量子芯片通过测量光量子态得到的随机数来加密信息。
优势在于:量子随机数生成芯片组通过生成不可预测且无模式的纯随机数,可以帮助智能手机用户安全地使用特定服务。
把随机数作为一个卖点,说明随机数还是挺重要的。